漫画:什么是冒泡排序算法?
面试官: 写一个冒泡排序吧
冒泡排序是一个比较经典和简单的排序算法,今天我们从从算法本身,时间复杂度以及稳定性方面来看看冒泡排序,这些方面也是研究其他排序算法的一般思路
一、冒泡思想
在算法国内,相传有一位大师,他不喜做官,在民间传道受业,弟子三千,人称“克”
有一天,克带着得意弟子谦子去溪边游玩,看到许多大大小小的石头在溪边,克拿起了四个大小不同的石子,摆成一行,如下:
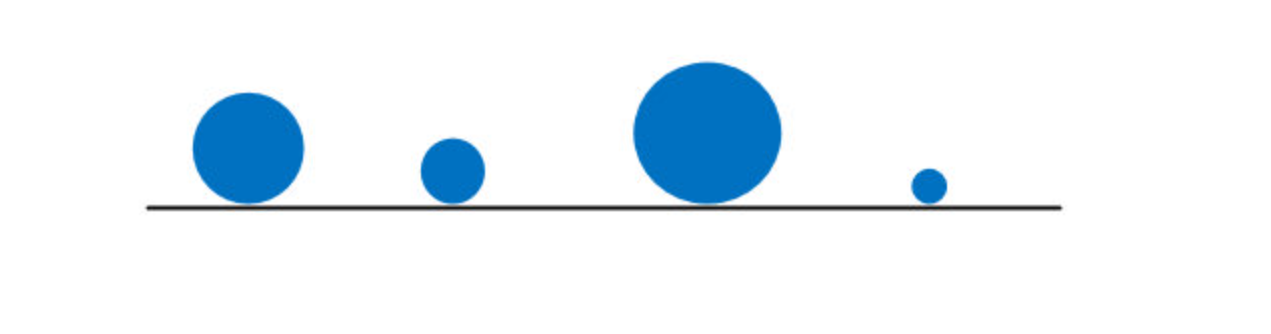
问:“谦子,你如何将这些石子按照从小到大的顺序从左到右依次排列成一行?”
“先找出最大的放在右边,然后再找出次大的,放在最大的左边,按照这个规律就可以依次排好了”,谦子回答道
“那你如何找到最大的呢?”,克问道
“用肉眼看”,谦子弱弱的说了一句
“怎么可以用肉眼看,如果成千上万你也用肉眼看吗?咱们算法国以算法著称,就是让一切问题的解决都可以最终化为一个算法,可以用程序写出来”,克严厉地批评道
“那该如何找最大的呢?”,谦子问道
“你看那水中的鱼,他们时不时地吐出泡泡,那泡泡越往上走就会越大

我们可以借鉴这种思路
从第一个石子开始,让它和右边相邻的石子进行比较,如果左边的石子大于右边的石子,那么就交换两个石子的位置,(也可以左小于右交换,这里采用大于交换),这样每比较一次,大的就跑到右边,直到跑到最右边”,克说道
克看谦子不明白,于是说:“起始时,左下标指向第一个石子,右下标指向第二个石子,然后比较”,说着说着画了一个图
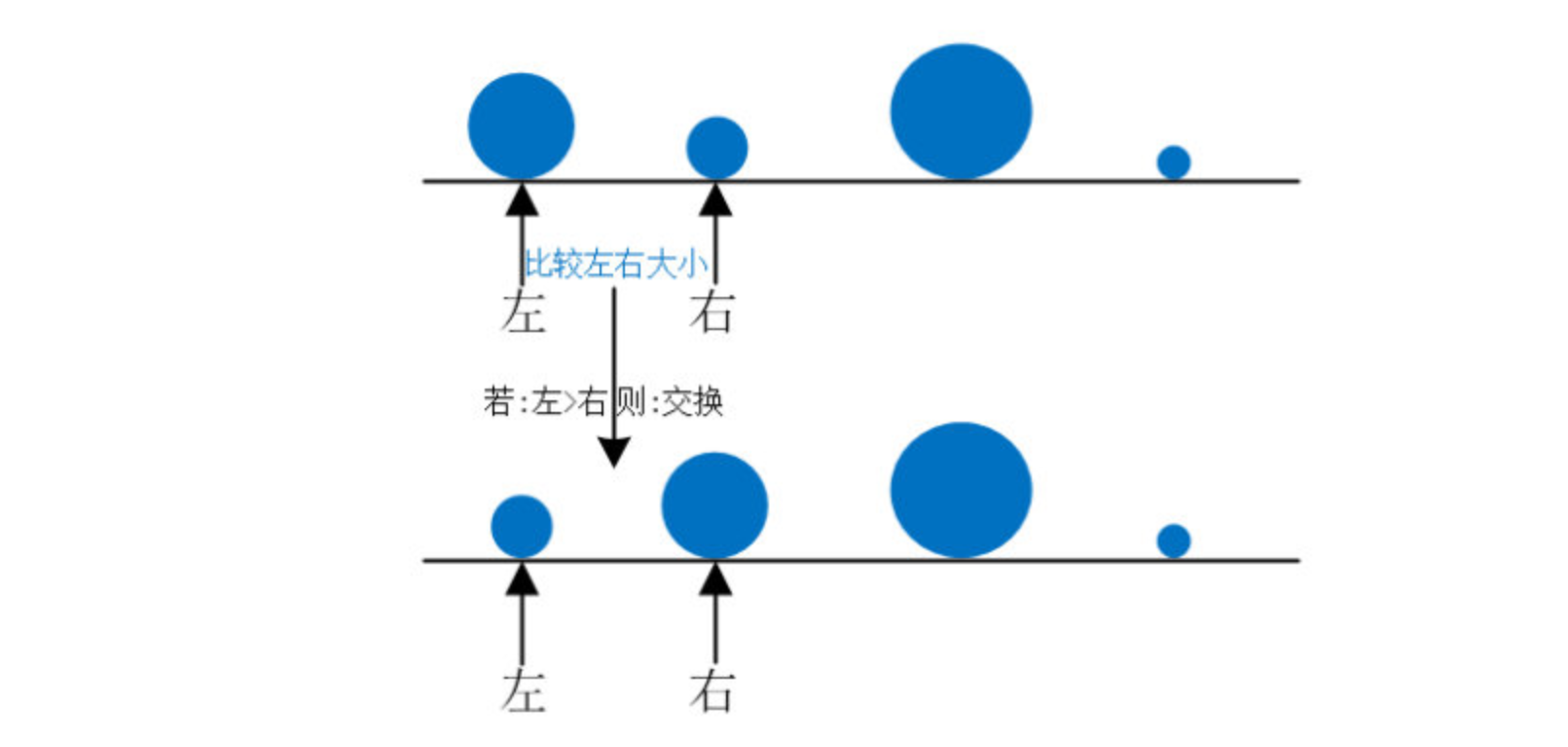
“然后左右下标同时向右移动,再次比较”,克接着说道,手不停的画着
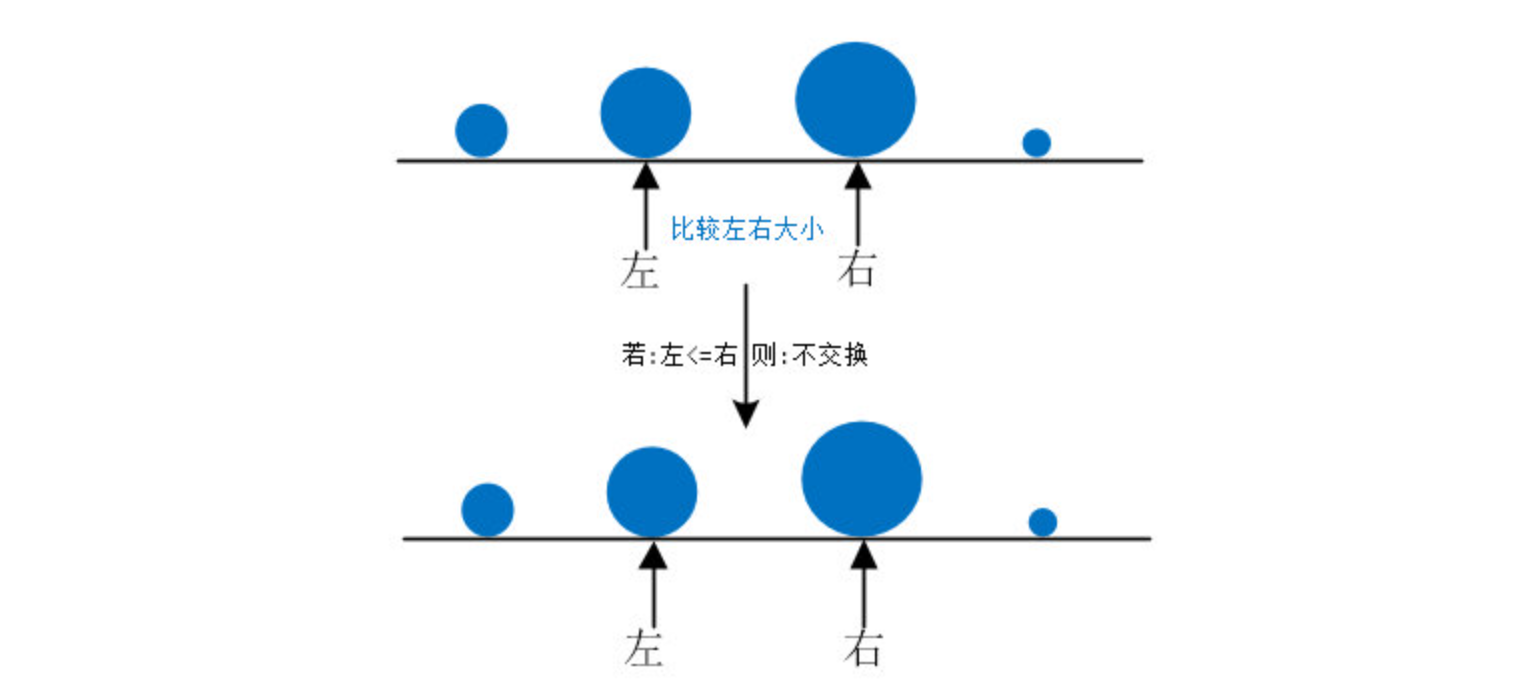
“这样一来,每次比较完,右下标指向的石头就是已经比较过的元素中的最大元素”,克微微笑了一下,看了看谦子,然后又画了一个图
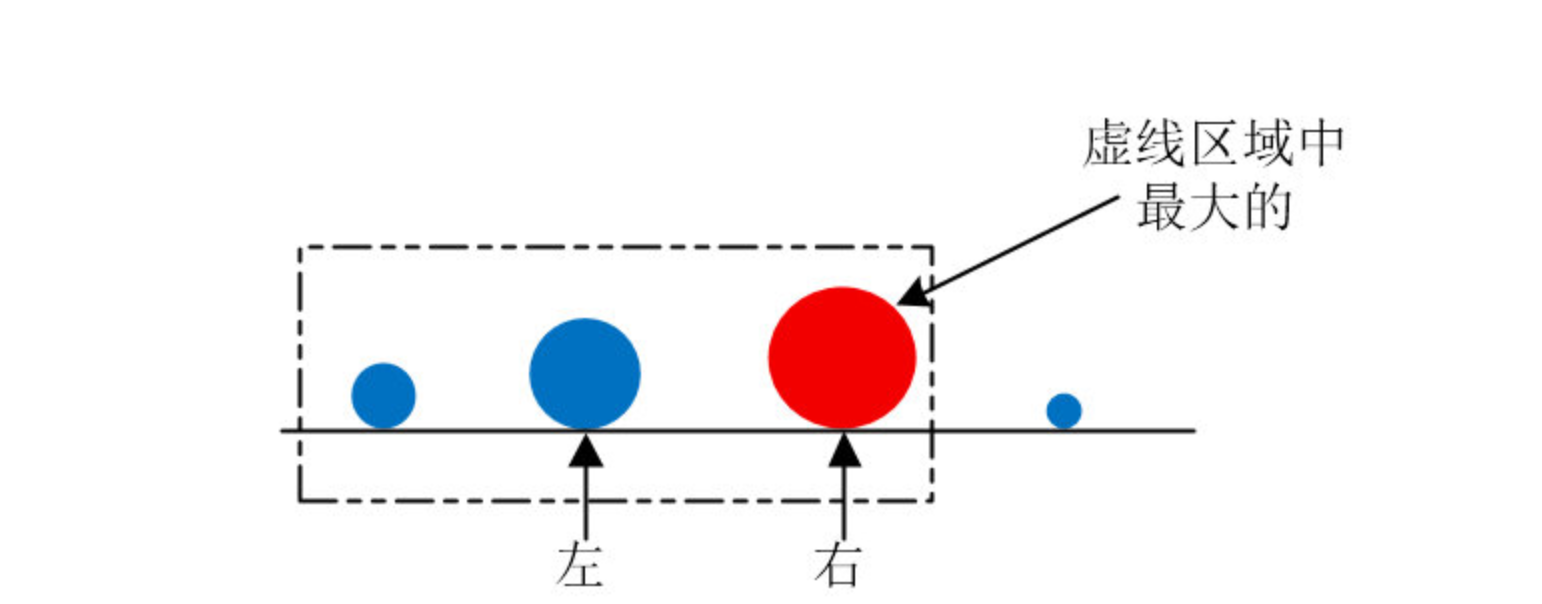
“按照这个做法,这一趟下来所有石子中最大的就跑到最右边了”,谦子悟出了其中的真谛,接着老师的话说了一句,自己在地上也画了一个图
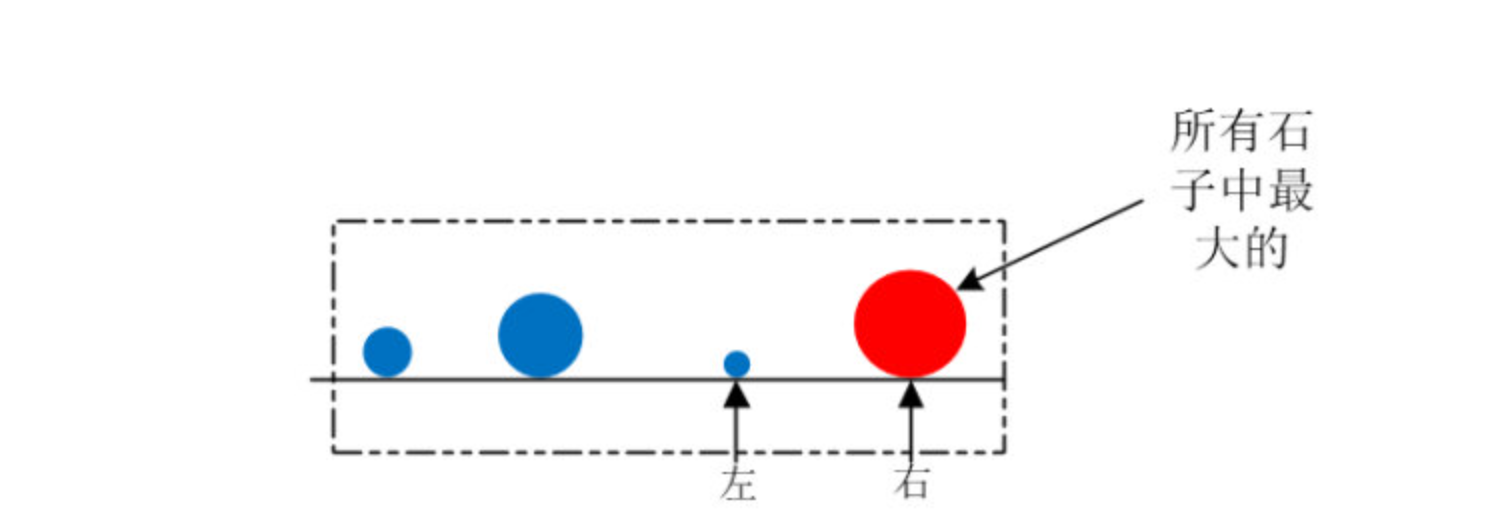
“这是第一趟排序,经过这趟排序之后,最大的就在最右边了,也就是排好序了,那么接下来就从剩下的三个石子中选最大的了,规则就和上面的一样了”,谦子继续说道,并画了一个图
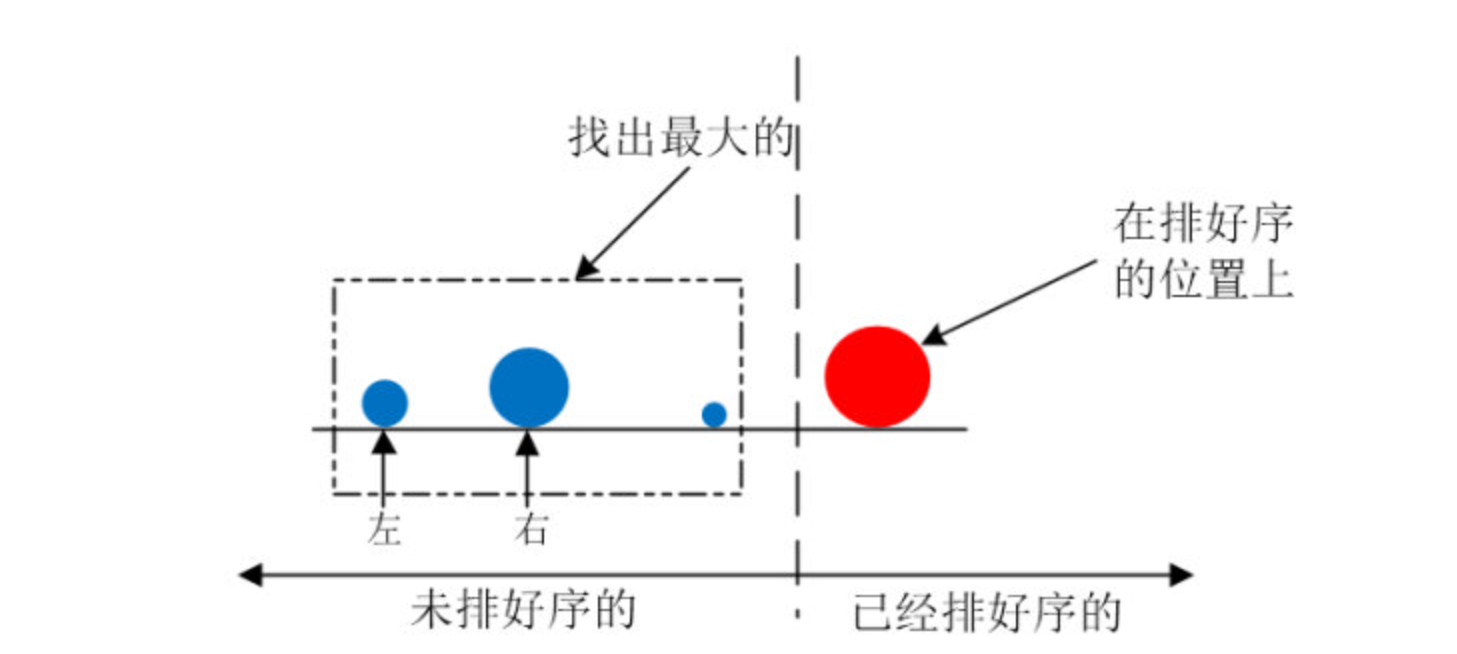
克脸上露出满意的笑容
然后克问,如果有 N 个石子,称从左到右找最大为一趟,那么要排好序需要多少趟?
谦子想了想,说道:“需要N-1次,因为如果因为N-1个数都排好了,那么最后一个数也就不用排了”,顺便画了一个图演示刚才四个石子的情况
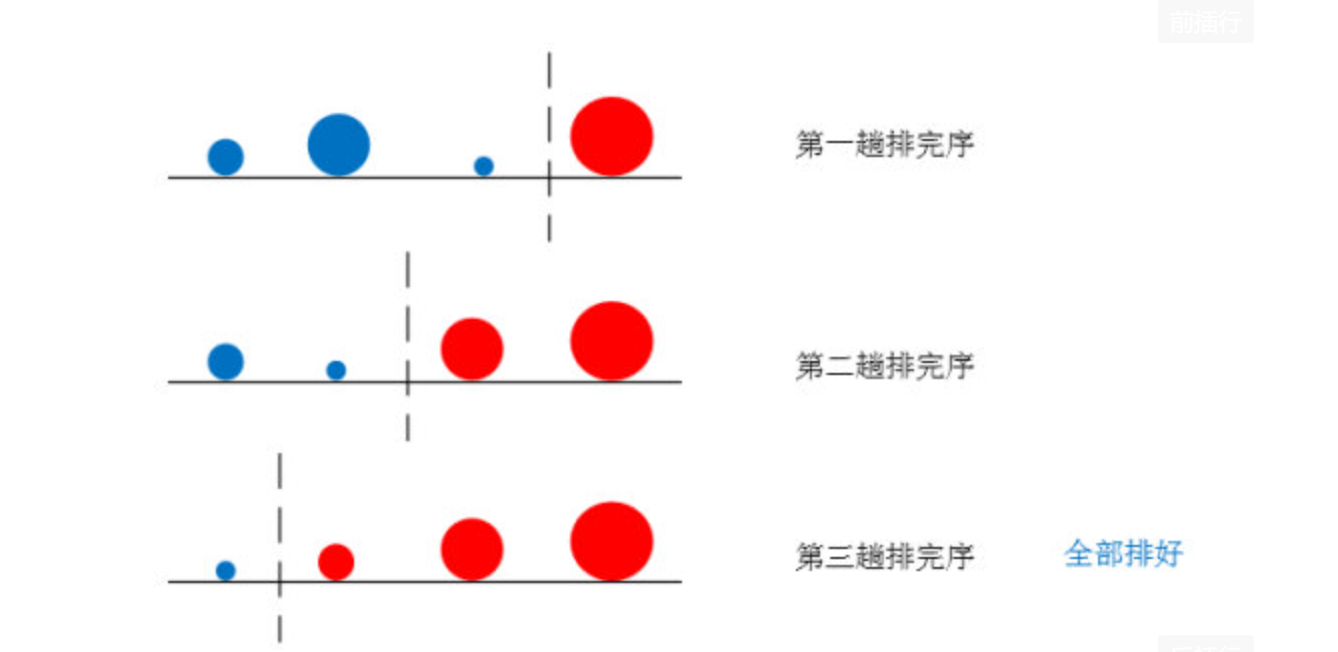
二、冒泡代码
“那你能把这个过程用代码实现吗?”,克问道
“这个。。。”,谦子挠了挠头,傻傻地笑了一下,克看了谦子一眼,转而在地下飞速地写了短短的几行代码
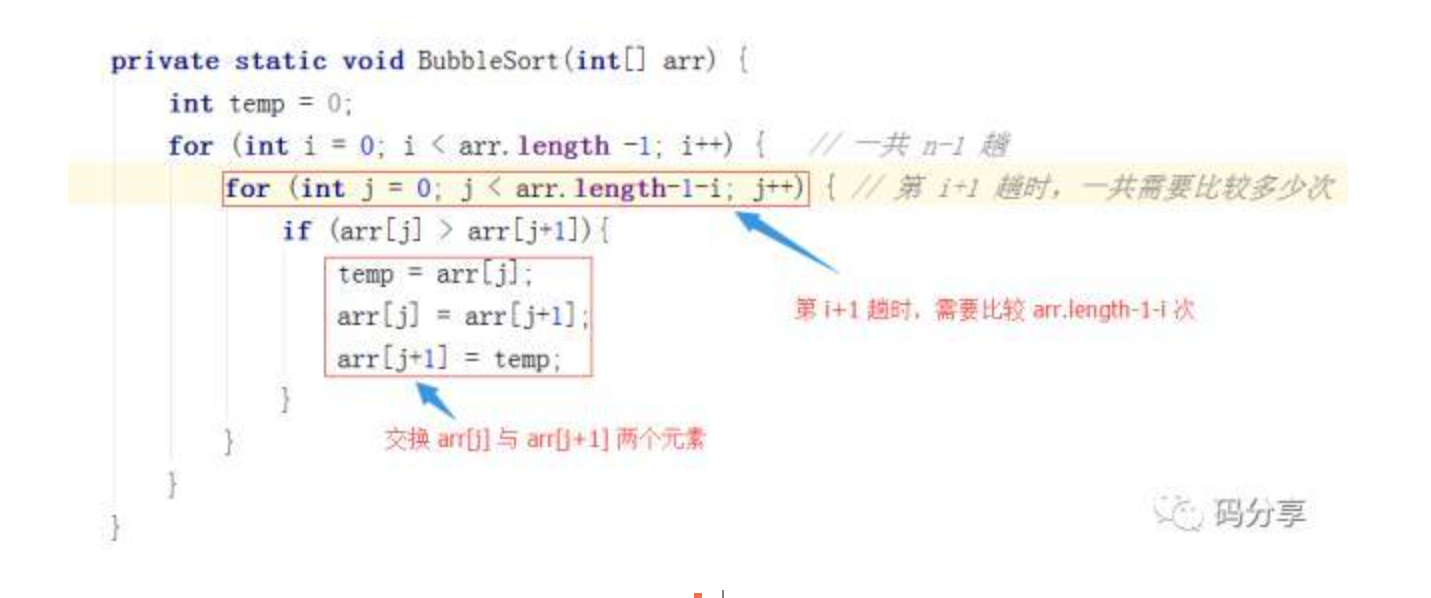
谦子心中暗暗惊叹老师的功力
“这个第一层循环是控制趟数,第二行能具体讲讲吗?”,谦子笑了笑问道
“第二层就是控制你第 i+1趟(因为i从0开始)所比较的次数,第 i +1 趟比较了 N – 1 -i 次”,克说道,最后画了两张图
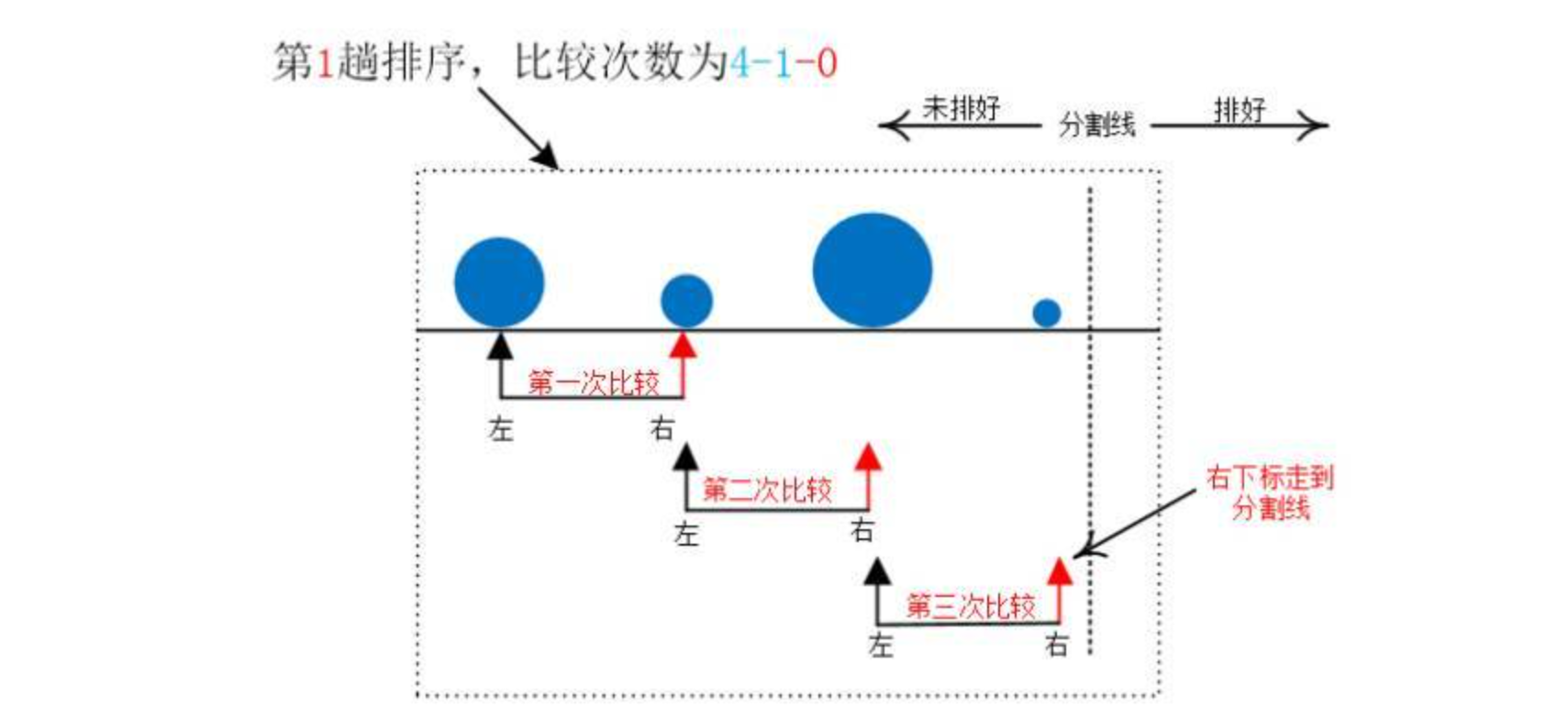
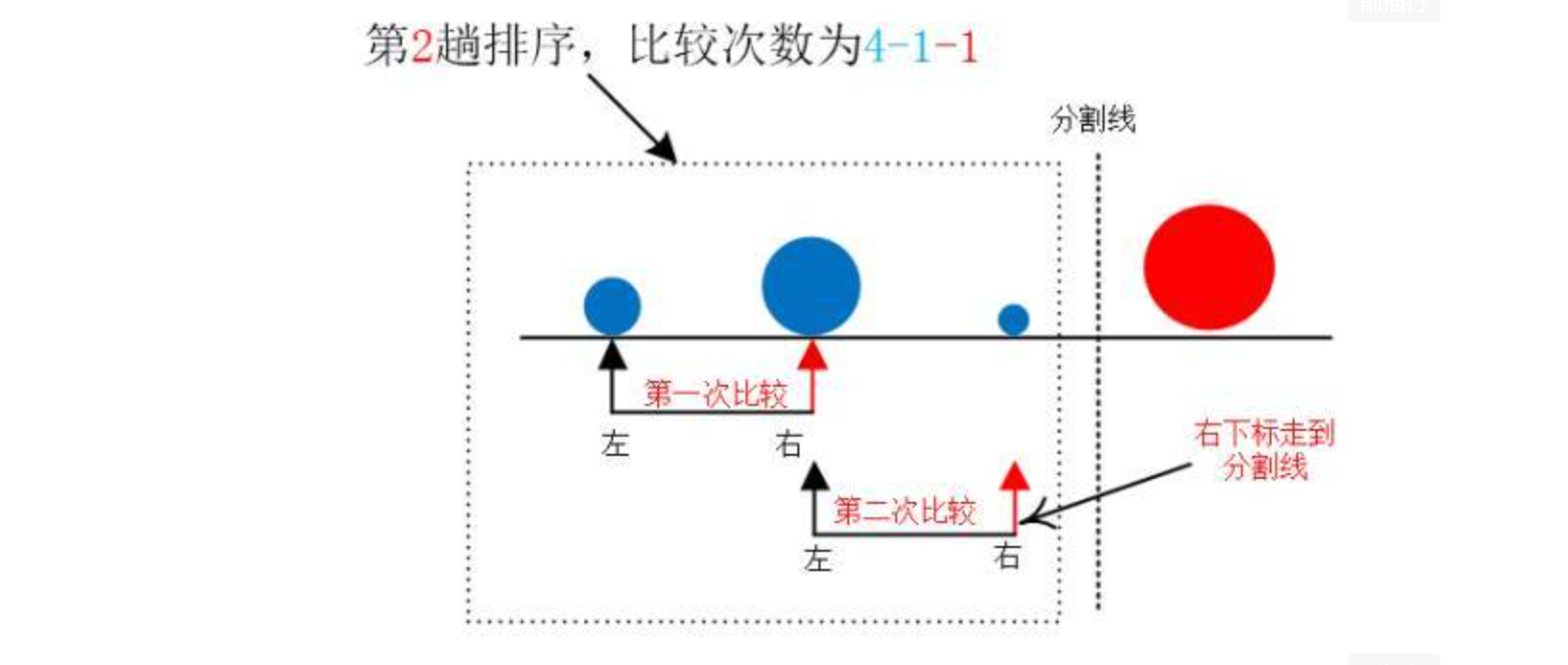
“随着趟数的增加,比较的次数也随之减小,这个规律很容易发现吧”,克说道
谦子点了点头
三、时间复杂度
“那你说说这个算法的时间复杂度吧”,克问道
谦子心里想到:
既然排序完需要3趟,第一趟需要比较3次,第二趟需要比较2次,第三趟需要比较1次,那一共比较了 3 + 2 + 1 次
那推广到数量为 n 的规模的话,那就需要 (n-1) + (n-2) +…+2+1 次,这不就是一个等差数列吗,很显然:

根据复杂度的规则,去掉低阶项(也就是n/2),并去掉常数系数,那复杂度就是O(n^2)了
“O(n^2)”,谦子想了一会说道
“恩恩,不错”,克说道
四、稳定性
“那这个算法稳不稳定呢?”,克又问道
“哦,什么是稳定性?”,谦子问道
“哦,这个还没有给他讲”,克忽然想起来
“所谓稳定性,其实就是说,当你原来待排的元素中间有相同的元素,在没有排序之前它们之间有先后顺序,在排完后它们之间的先后顺序不变,我们就称这个算法是稳定的”,克说道,顺便画了一个图举了一个例子
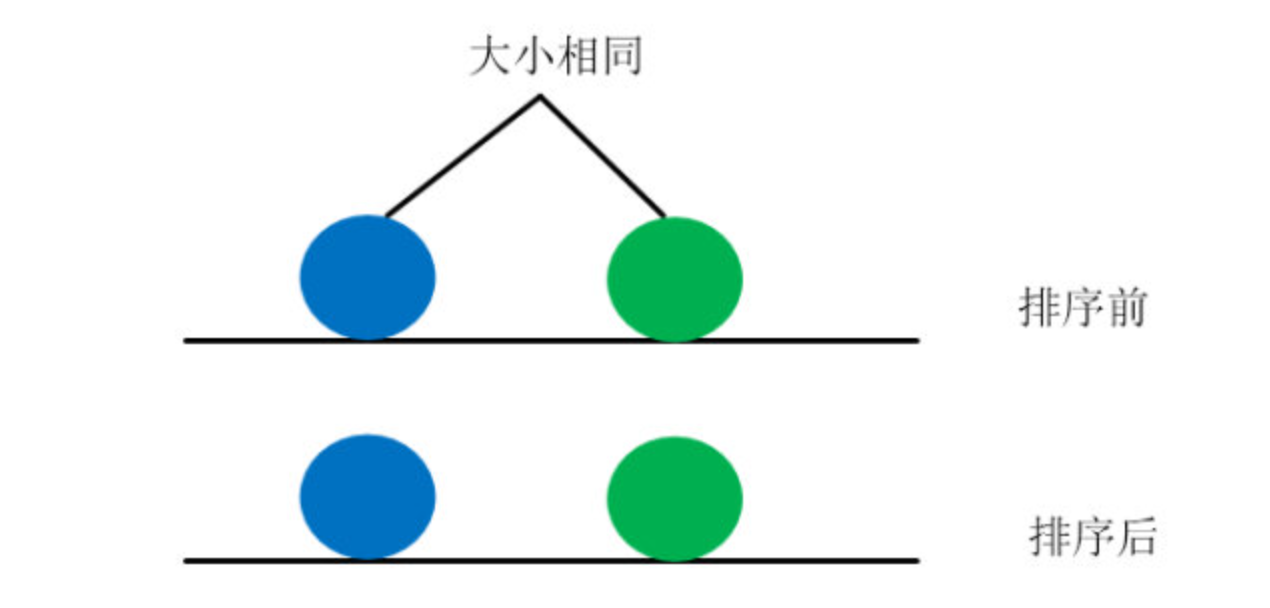
“看到了吧,原本同样大的石子,蓝色的在绿色的左边,拍完序后蓝色的仍然在绿色的左边,这就是稳定的”,克解释道
“哦,我懂了,那冒泡排序就是一个稳定的排序了,因为在交换的时候,如果两个石子相同,那么就不交换[if (arr[j] > arr[j+1]){ 交换}],相同元素不会因为算法中哪条语句相互交换位置的”
“恩恩,对的”,克说道
天色渐晚,克和弟子走在了回去的路上,回去的路上克告诉谦子今天的排序算法叫冒泡排序
### 五、优化一下冒泡排序的算法
假如从开始的第一对到结尾的最后一对,相邻的元素之间都没有发生交换的操作,这意味着右边的元素总是大于等于左边的元素,此时的数组已经是有序的了,我们无需再对剩余的元素重复比较下去了。
代码如下:
public static int[] bubbleSort(int[] arr) {
if (arr == null || arr.length < 2) {
return arr;
}
int n = arr.length;
for (int i = 0; i < n; i++) {
boolean flag = true;
for (int j = 0; j < n -i - 1; j++) {
if (arr[j + 1] < arr[j]) {
flag = false;
int t = arr[j];
arr[j] = arr[j+1];
arr[j+1] = t;
}
}
//一趟下来是否发生位置交换
if(false)
break;
}
return arr;
}

评论(5)
优化的第一个代码,第一个for循环为什么是i<n 而不是i<n-1-1
我写错了,应该是i<n-1
i < n 和 i < n – 1 都是可以滴。问题不大,我改成 i < n – 1 吧
那里不是flag嘛?
哈哈,已更改,谢谢提醒