MySQL 索引(一)
- 你了解索引吗?
- 常见的索引的数据结构有哪些?各自有什么优缺点?
- 为什么 MySQL 采用 B+ 树作为索引?有哪些好处?
- B+ 树和 B 树相比,有什么优点?
什么是索引
提到索引,我想大家肯定都不陌生了。在讲专业术语之前,我们先来看个例子。
你在一个巨大的图书馆,里面摆满了成千上万本书。当你想要找一本特定的书时,如果没有任何指引,你可能需要一本一本去翻找,这会耗费大量的时间和精力。但如果这个图书馆有一套完善的分类系统和目录,你可以先通过目录快速定位到你想要的书可能在哪个区域,然后再在那个区域里进一步查找,这样就会高效得多。
索引,简单来说,就是数据库中用于提高数据检索速度的数据结构。
在 MySQL 数据库中,索引就像是图书馆的目录。当数据库中有大量的数据时,如果没有索引,要找到特定的数据就如同在没有目录的图书馆中找书一样困难。而有了索引,就可以快速地定位到所需的数据,大大提高查询的效率。
索引常见的数据结构
下面我们来学习一些常见的索引的数据结构,然后分析一下它们的区别。看完这几种数据结构之后,你就能对索引有一个整体的把握了。
哈希
第一种是哈希索引,它是一种以哈希表为基础的数据结构。
定义就是通过哈希函数将索引键值映射到一个特定的位置,从而快速定位数据。简单来说,就像是给数据分配一个独特的 “地址”,当你要找这个数据的时候,通过这个地址就能快速找到它。
具体实现上,首先要有一个哈希函数,这个函数会根据输入的键值计算出一个哈希值。然后,根据这个哈希值将数据存储到哈希表的特定位置。当要查找数据时,再次使用哈希函数计算键值的哈希值,然后直接去对应的位置查找数据。
下面我们来看一个例子,假设我们有一个用户信息表是这样的,左边是身份证号,右边是用户名:
| ID Card Number | Name |
|---|---|
| 110101198001011234 | Alice |
| 110101198505062345 | Bob |
| 120103199306153456 | Charlie |
| 110101198001011111 | David |
| 110101198505063456 | Emily |
我们希望通过用户的 身份证号 (ID Card Number) 来快速查找到对应的 姓名 (Name)。为了提高查询效率,我们为身份证号字段建立 哈希索引。
建立索引之后,系统会对身份证号通过一个哈希函数(例如 hash(ID Card Number) % N ,N 是哈希表的桶数)进行计算,生成一个哈希值,然后根据哈希值将数据映射到对应的桶中。
假设哈希表大小为 5 个桶,编号为 0~4 。
身份证号经过哈希函数计算后,结果如下:
| ID Card Number | Name | 哈希值 | 桶编号 (Bucket) |
|---|---|---|---|
| 110101198001011234 | Alice | 1 | Bucket 1 |
| 110101198505062345 | Bob | 2 | Bucket 2 |
| 120103199306153456 | Charlie | 3 | Bucket 3 |
| 110101198001011111 | David | 1 | Bucket 1 |
| 110101198505063456 | Emily | 3 | Bucket 3 |
现在我们希望查找身份证号 110101198001011111 对应的用户姓名。
系统首先会使用哈希函数进行计算,得出一个哈希值 hash(110101198001011111) % 5 = 1,从而定位到 Bucket 1。
然后再去查找桶中的数据,但是,此时 Bucket 1 中有两个身份证号:110101198001011234 和 110101198001011111。其实,这就是我们常说的哈希冲突。
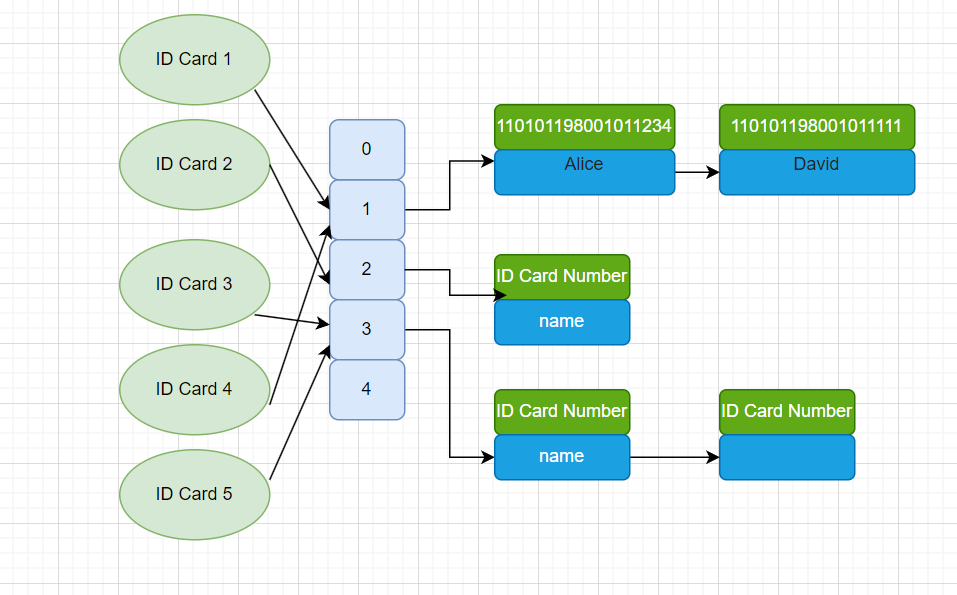
这个时候,哈希索引就会在冲突的桶位中引入链表,存储发生冲突的数据,来解决这个问题。
最后,系统会对桶中的记录逐一比对,找到身份证号为 110101198001011111 的用户,姓名为 David。
总的来说, 哈希索引适用于等值查询的场景,查询速度快,只需要计算哈希值并定位到桶,大多数情况下查询时间接近 O(1)。
但是,如果哈希表的桶数量过少或哈希函数设计不合理,冲突会增多,导致链表长度增加,从而降低查询效率。
另外,哈希索引是不支持范围查询的,例如 WHERE ID Card Number > 110101198001011000。这种情况下,就只能进行全表扫描,效率是非常低的。
有序数组
上面我们说到,哈希索引是不支持范围查询的。而有序数组,就可以解决这个问题。它不仅支持等值查询,还支持范围查询。
有序数组索引是一种基于 有序数组 的索引模型。它将索引值按照 升序或降序 排列,适合用于静态数据(即数据写入后基本不更新)。它的查询效率高,特别适合范围查询,但在涉及频繁的插入、删除和更新操作时,效率就很低了。
有序数组索引的结构就是,数据按照键值(Key)从小到大存储在一个有序数组中,然后索引值(Key)通过数组的位置来快速定位数据。因为数组是有序的,所以它支持二分查找,查询效率为 O(log n)。
假设我们有一个学生表,记录了学生的 ID 和姓名。
| 学生ID(Student ID) | 姓名(Name) |
|---|---|
| 1 | Alice |
| 3 | Bob |
| 5 | Charlie |
| 7 | David |
| 9 | Emily |
比如,我想查找学生 ID 为 5 的姓名,使用二分查找的话,初始范围为 [1, 9] ,中间值为 5 。那么就匹配成功了,返回 Charlie。
再比如,我想查询范围 ID 在 3~7 的学生,因为数组是有序的,可以直接定位 3 和 7 的位置,然后顺序读取中间数据就可以了。
总之,有序数组的的查找速度很快,使用二分查找,查询效率为 O(log n),比哈希索引要慢一点。但是对范围查询很友好,例如 WHERE ID > 5 AND ID < 10。另外,有序数组中,数据存储的很紧凑且按照顺序排列,占用的存储空间小,存储效率高。
但是,它不适合动态数据,因为插入、删除操作需要移动大量元素,时间复杂度都是 O(n),效率是很低的,特别是在数据量很大的情况下。而且维护数组的成本也比较高,这是因为,当数据频繁更新时,需要维护数组的有序状态。
二叉搜索树
基于有序数组插入和删除效率低的缺点,我们再来看看二叉搜索树。
二叉搜索树(Binary Search Tree,简称 BST)索引是一种基于二叉树结构的索引模型。二叉搜索树的特点是每个节点最多有两个子节点,并且遵循以下规则:
- 左子树的所有节点值小于根节点值。
- 右子树的所有节点值大于根节点值。
- 每个子树本身也是一棵二叉搜索树。
通过这种结构,可以快速进行查找、插入和删除操作,二叉搜索树比较适合动态数据的存储。
下面来看一下二叉搜索树中的操作:
- 查找:从根节点开始比较,如果目标值小于当前节点值,则进入左子树;如果大于,则进入右子树;如果相等,则查找成功。
- 插入:插入时,根据值的大小确定插入位置,保证树的结构依然满足二叉搜索树的性质。
- 删除:需考虑三种情况:
- 删除的是叶子节点(直接删除即可)。
- 删除的节点只有一个子节点(让子节点替代删除节点的位置)。
- 删除的节点有两个子节点(用右子树的最小值或左子树的最大值替代该节点)。
下面我们再来看一个例子:
在一个学生成绩管理系统中,记录学生的分数和姓名,我们需要快速查找某个分数对应的学生,或者查询分数范围内的所有学生。
我们有如下数据:
| 分数(Score) | 姓名(Name) |
|---|---|
| 80 | Alice |
| 60 | Bob |
| 90 | Charlie |
| 70 | David |
| 85 | Emily |
我们利用这些数据来组成一棵二叉搜索树,这棵树就是这样的:
80 (Alice)
/ \
60 (Bob) 90 (Charlie)
\ /
70 (David) 85 (Emily)
如果我想查找分数为** 85 **的学生:
- 从根节点 80 开始,85 > 80,进入右子树。
- 到达节点 90,85 < 90,进入左子树。
- 到达节点 85,找到对应的学生 Emily 。
再比如,我想查找分数范围在** 70~85 **的学生:
- 从根节点 80 开始,70 <= 80 <= 85,符合条件,加入结果集。
- 进入左子树,找到 60,不在范围内,跳过。
- 左子树继续向右,找到 70,符合条件,加入结果集。
- 回到根节点,进入右子树,找到 90,大于范围最大值,停止遍历右子树。
- 继续向左找到 85,符合条件,加入结果集。
- 最终结果:[70 (David), 80 (Alice), 85 (Emily)] 。
但是,让我们来考虑一种极端情况,假设我们需要按照分数构建一个二叉搜索树,分数和对应的学生姓名如下:
| 分数(Score) | 姓名(Name) |
|---|---|
| 10 | Alice |
| 20 | Bob |
| 30 | Charlie |
| 40 | David |
| 50 | Emily |
那么构造出来的二叉搜索树就是这样的:
10 (Alice)
\
20 (Bob)
\
30 (Charlie)
\
40 (David)
\
50 (Emily)
在这种情况下,这棵树就退化成一个链表了。
让我们来总结一下,二叉搜索树查找效率高,平均时间复杂度为 O(log n),比较适合动态数据的存储和查询。但是,它没有平衡机制,如果每次插入的元素都是二叉搜索树中最大的元素,那么这棵树就会退化成链表,查找的效率就降为 **O(n) **了。
平衡二叉搜索树
为了解决二叉搜索树在极端情况下退化成链表的问题,就有了平衡二叉搜索树的概念。
平衡二叉树(Balanced Binary Tree),也称 AVL 树,是一种特殊的二叉搜索树,特点是能够通过维护自身的平衡性,避免退化为链表,确保在最坏情况下的操作效率仍然为 O(log n)。
平衡性是什么意思呢?
就是说,对于一棵平衡二叉树,任意节点的左右子树高度差(平衡因子)不超过 1。
平衡因子 = 左子树高度 – 右子树高度
我们来看一个例子就明白了。
假设我们有一组数据:10, 20, 30 ,按顺序插入到一棵空的 AVL 树。
- 首先,插入 10:
此时树为空,直接插入 10 ,它成为根节点。
- 然后,再插入 20:
因为 20 > 10,所以成为 10 的右子节点。
此时,左子树高度为 0,右子树高度为 1,平衡因子 = 0 – 1 = -1,树的平衡因子仍然满足要求。
- 最后,再插入 30:
因为 30 > 10 ,进入右子树。
因为 30 > 20,成为 20 的右子节点。
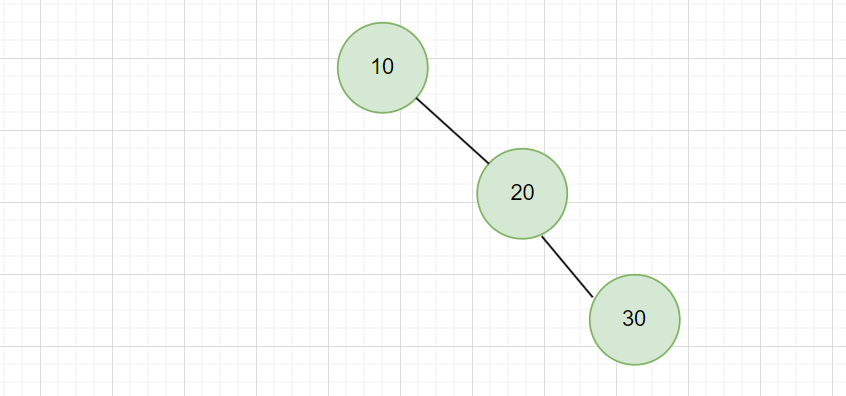
注意,现在左子树高度为 0,右子树高度为 2。那么根节点 10 的平衡因子为 -2,就不满足平衡性了,所以树的平衡就被打破了。
为了恢复平衡,它会进行一次 左旋操作。即以 20 为中心旋转,10 成为 20 的左子节点。
调整后的树为:
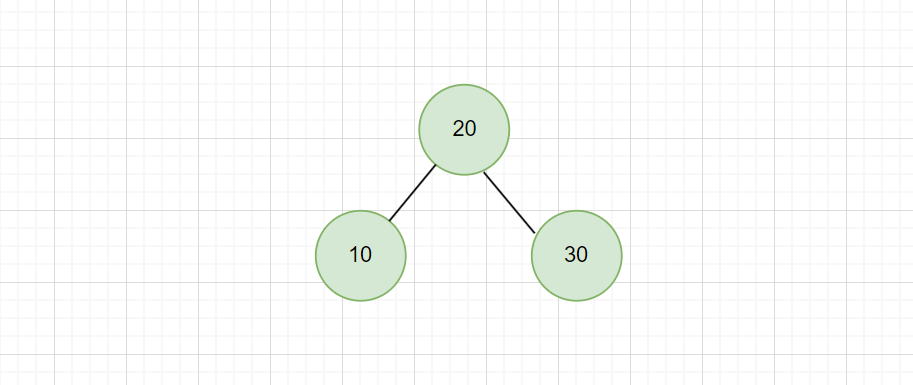
现在树重新变为平衡状态,所有节点的平衡因子均满足要求。
通过在极端的情况下构造这棵树,我们可以看到,平衡二叉搜索树可以始终保持树的高度为 O(log n),确保查找、插入和删除的效率。保证了在最坏情况下,也能在对数时间内完成操作。
B树
但是,我们再来思考一个问题,无论是二叉搜索树还是平衡二叉搜索树,它们都是二叉树,每个节点都只能有两个子节点。如果数据非常多,那么二叉树的高度就会很高。
需要知道的是,在数据库和文件系统中,树的高度和磁盘 I/O 次数直接相关。
因为每访问一个节点,就意味着需要从磁盘中读取对应的数据页(一个数据块),这是一次磁盘 I/O 操作。因此,树的高度决定了查找时需要的 I/O 次数。
也就是说,树的高度越高,访问的节点数越多,磁盘 I/O 次数越多,性能就越差。
所以为了解决二叉树存储数据少的情况,就有了 B 树。
什么是 B 树呢?
B树(Balanced Tree) 是一种 平衡的多路搜索树。在 B 树中,每个节点可以拥有多个子节点。这种设计减少了树的高度,从而降低了磁盘的 I/O 次数。
如果一棵 B 树中,每个节点可以拥有三个子节点,那么这棵树就叫做三阶 B 树。
举个例子,如果数据量为 1000000 ,二叉搜索树的高度为 log₂(1000000) ≈ 20 ,3阶 B树的高度为 log₃(1000000) ≈ 13。树的高度低了,所以磁盘的 I/O 次数也就少了很多,对吧?
假设,现在有这些数据: 10, 20, 5, 15, 25, 30, 35 。
那么,构造出来的三阶 B 树就是这样的:
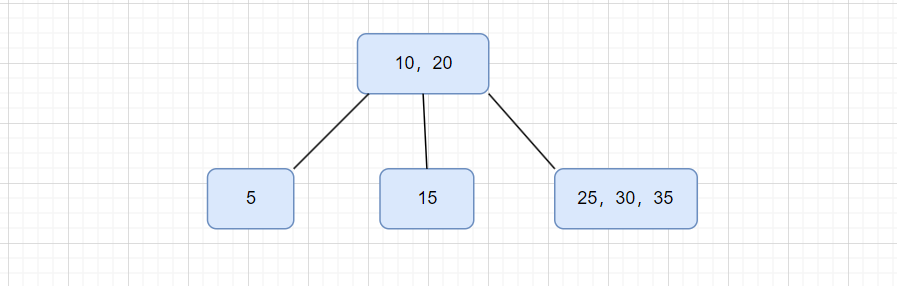
这里我们只需要大体了解 B 树是什么样就可以了。
看到这里,我们肯定会觉得 B 树已经很“优秀”了,既是有序的,还是平衡的,而且还解决了平衡二叉树的高度问题。
但是,B 树有一个很大的缺点,那就是 B 树的所有节点(包括叶子节点和非叶子节点)都存储了数据,这样就会导致每次查找都可能停留在非叶子节点读取数据。
这样说,大家可能听不明白,我们结合一个例子来看一下。
假设我们在一个电商系统中,有一个 订单表 (orders),存储了所有的订单数据,按订单编号 (order_id) 进行索引。我们现在需要在这个表中查询订单编号为 “20231227001” 的订单。
表结构是这样的:
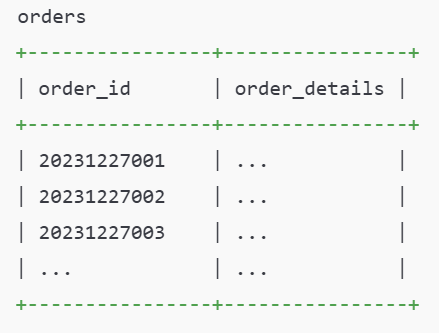
而且我们假设订单数据量非常大,总共有 1000万条订单,数据量非常庞大,这时需要依赖索引来快速查询数据。
此时,B 树是这样的:

假设 B 树的阶数为 4(每个节点最多包含 4 个子节点)
现在,我们要查询订单编号为 20231227001 的订单数据。
那么查询过程是这样的:
- 访问根节点
从磁盘中加载根节点 [3000 | 6000 | 9000] ,判断 20231227001 在第一个子树 [1000 | 2000] 中。 - 访问第一层子节点
加载 [1000 | 2000] 节点,最终在这个范围内找到了目标值。
由于非叶子节点也存储了数据,所以当我们查找一个值时,如果这个值在叶子节点,可能就会不可避免地读取到非叶子节点的数据,所以系统需要多次从磁盘中加载这些节点进行查询,这样就会增加磁盘 I/O 的次数,导致查询效率降低。
总之,B 树虽然解决了二叉树存储数据少的缺点,但是它自己本身也有一个缺点,那就是它在非叶子节点存储了数据,在查询数据时,有时会进行不必要的磁盘 I/O ,所以导致查询效率很低。
B+树
基于 B 树的缺点,我们再来看一下 B+ 树,B+ 树的结构是这样的:
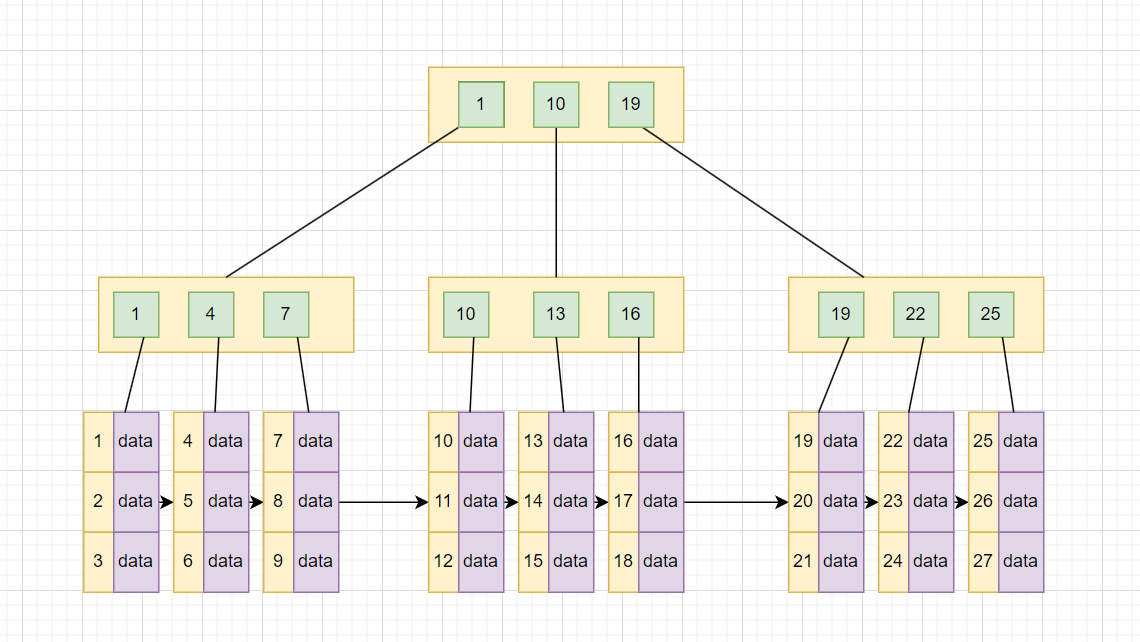
B+ 树有这么几个特点:
- 将所有数据都存储在叶子节点,而非叶子节点仅作为索引使用。 因此占用的空间更小。这意味着在同一层级的节点中,可以容纳更多的索引项,从而减少树的高度。树的高度降低后,从根节点到叶子节点的路径更短,查询时磁盘I/O次数减少,所以查询效率就更高。
- 所有叶子节点之间通过指针相互连接,形成一个有序链表。范围内的数据可以高效地从叶子节点链表中读取,避免回到上层节点查询。
第一点比较好理解。
第二点中,关于叶子节点之间的有序链表,我们来看一个例子就明白了。
假设有以下学生数据,我们按照学生 ID 作为索引构造一个三阶的B+树:
| 学生ID | 分数 |
|---|---|
| 1 | 85 |
| 2 | 90 |
| 3 | 78 |
| 4 | 92 |
| 5 | 88 |
| 6 | 76 |
| 7 | 95 |
| 8 | 89 |
我们用表中的数据来构造一棵 3 阶 B+ 树:
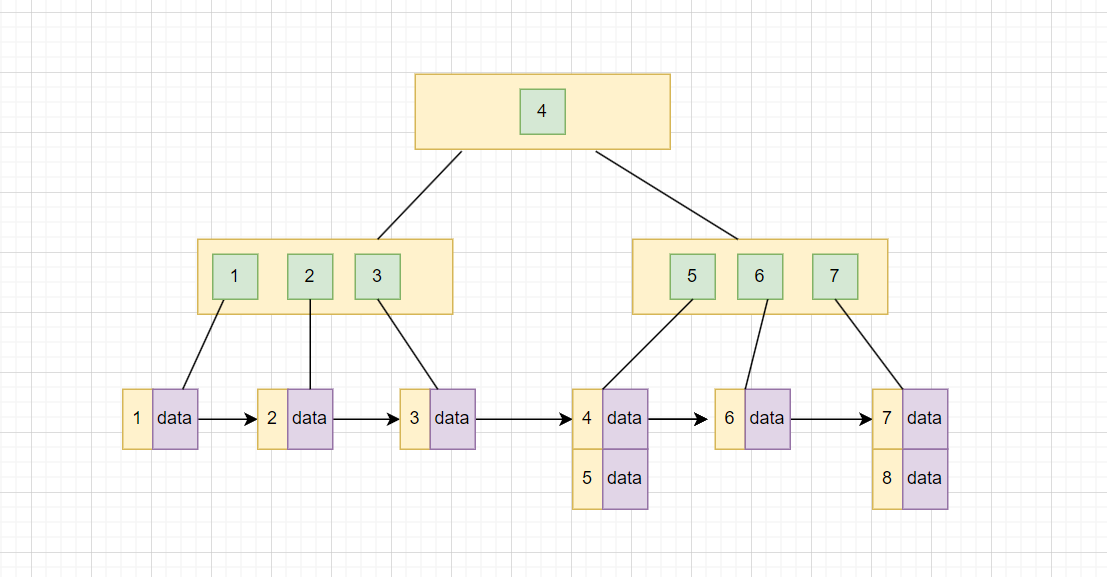
我先来解释一下这些节点:
- 根节点 4:
- 根节点的值是
4,表示索引的分裂点。小于等于4的学生ID存储在左侧,大于4的存储在右侧。
- 中间节点 [2 ,3] 和 [5 ,7]:
- 左子树
[2 3]:值是2和3,表示从1到3的数据范围。 - 右子树
[5 7]:值是5和7,表示从4到8的数据范围。
- **叶子节点 **:
- 叶子节点中保存了具体的数据,而且这些叶子节点通过链表连接起来,便于范围查询。
现在我们想要查询学生 ID 从 3 到 6 的分数,查询过程就是这样的:
- 从根节点
[4]开始:3 <= 4,进入左子树[2 3]。 - 在
[2 3]节点:3的范围在此分裂点,找到叶子节点[3]。 - 通过叶子节点链表,顺序访问
[3] -> [4 5] -> [6],直到结束。
这种方式避免了全表扫描,通过树的层级和叶子链表结合实现了高效的范围查询。
再来总结一下B+ 树和 B 树的区别:
| 特性 | B 树 | B+ 树 |
|---|---|---|
| 数据存储位置 | 所有节点(非叶子节点和叶子节点)都存储数据 | 只有叶子节点存储数据,非叶子节点仅存索引 |
| 叶子节点连接 | 叶子节点之间无序,无额外连接 | 叶子节点通过链表有序连接,便于范围查询 |
| 查询效率 | 查询时可能需要在叶子节点和非叶子节点中查找 | 查询时只需要访问叶子节点,效率更高 |
| 空间利用率 | 较低,因为非叶子节点也存储数据 | 较高,因为非叶子节点仅存索引 |
| 范围查询性能 | 较差,需要回溯树结构 | 较好,直接在叶子节点的链表中顺序扫描 |
总而言之,B+树的特点,就是它的非叶子节点只存储了索引,不存储实际数据,所以避免了不必要的查询;另外,叶子节点存储数据,并且叶子节点之间通过链表来进行连接,是有序的,这样就非常方便进行范围查询。
总结
通过这篇文章,我们了解了什么是索引,以及索引的常见模型,并且知道了每个索引模型的优点和缺点,还知道了是怎么从最普通的数组一步步演化成 B+ 树的,这部分内容可能听起来有一些枯燥,但是我们应该多花一些时间去理解这些模型,因为这些都是很基础的东西,也为我们以后更好的学习数据库的内容做一个铺垫。好啦,这篇文章就先写到这里啦!
