从中序与后序遍历序列构造二叉树 🌟🌟🌟🌟中等
课后作业
问题描述
原文链接:106. 从中序与后序遍历序列构造二叉树
难度中等
1018
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:
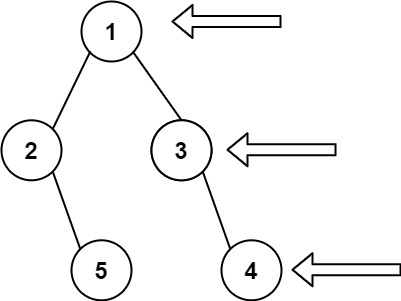
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]
提示:
1 <= inorder.length <= 3000postorder.length == inorder.length-3000 <= inorder[i], postorder[i] <= 3000inorder和postorder都由不同的值组成postorder中每一个值都在inorder中inorder保证是树的中序遍历postorder保证是树的后序遍历
代码实现
Java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
Map<Integer, Integer> map = new HashMap();
public TreeNode buildTree(int[] inorder, int[] postorder) {
for(int i = 0;i < inorder.length; i++){
map.put(inorder[i], i);
}
return f(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1);
}
TreeNode f(int[] in, int l1, int r1, int[] post, int l2, int r2){
if(l1 > r1 || l2 > r2){
return null;
}
TreeNode root = new TreeNode(post[r2]);
int i = map.get(post[r2]);
root.left = f(in, l1, i - 1, post, l2, l2 + (i-l1) - 1);
root.right = f(in, i + 1, r1, post, l2 + (i-l1) , r2 - 1);
return root;
}
}
Python
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def buildTree(self, inorder, postorder):
"""
:type inorder: List[int]
:type postorder: List[int]
:rtype: TreeNode
"""
hashMap = {}
for i in range(len(inorder)):
hashMap[inorder[i]] = i
return self.f(inorder, 0, len(inorder)-1, postorder, 0, len(postorder)-1, hashMap)
def f(self, ino, l1, r1, post, l2, r2, hashMap):
if l1 > r1 or l2 > r2:
return None
root = TreeNode(post[r2])
i = hashMap[post[r2]]
root.left = self.f(ino, l1, i-1, post, l2, l2+(i-l1)-1, hashMap)
root.right = self.f(ino, i+1, r1, post, l2+(i-l1), r2-1, hashMap)
return root
C++
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
unordered_map<int, int> map;
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
for (int i = 0; i < inorder.size(); i++) {
map[inorder[i]] = i;
}
return f(inorder, 0, inorder.size()-1, postorder, 0, postorder.size()-1);
}
TreeNode* f(vector<int>& in, int l1, int r1, vector<int>& post, int l2, int r2) {
if (l1 > r1 || l2 > r2) {
return nullptr;
}
TreeNode* root = new TreeNode(post[r2]);
int i = map[post[r2]];
root->left = f(in, l1, i-1, post, l2, l2+(i-l1)-1);
root->right = f(in, i+1, r1, post, l2+(i-l1), r2-1);
return root;
}
};
Go
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func buildTree(inorder []int, postorder []int) *TreeNode {
hashMap := make(map[int]int)
for i := 0; i < len(inorder); i++ {
hashMap[inorder[i]] = i
}
return f(inorder, 0, len(inorder)-1, postorder, 0, len(postorder)-1, hashMap)
}
func f(ino []int, l1 int, r1 int, post []int, l2 int, r2 int, hashMap map[int]int) *TreeNode {
if l1 > r1 || l2 > r2 {
return nil
}
root := &TreeNode{Val: post[r2]}
i := hashMap[post[r2]]
root.Left = f(ino, l1, i-1, post, l2, l2+(i-l1)-1, hashMap)
root.Right = f(ino, i+1, r1, post, l2+(i-l1), r2-1, hashMap)
return root
}
