平衡二叉树 🌟🌟🌟🌟🌟简单
课后作业
问题描述
原文链接:110. 平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例 1:
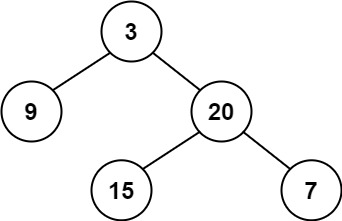
输入:root = [3,9,20,null,null,15,7]
输出:true
示例 2:
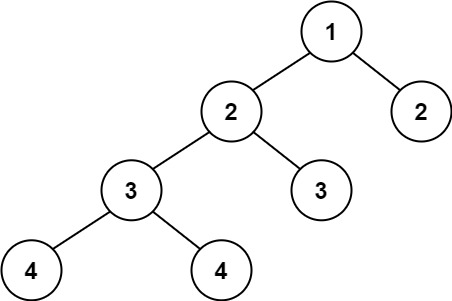
输入:root = [1,2,2,3,3,null,null,4,4]
输出:false
示例 3:
输入:root = []
输出:true
提示:
- 树中的节点数在范围
[0, 5000]内 -104 <= Node.val <= 104
代码实现
Java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
// n!
// 优化版本
public boolean isBalanced(TreeNode root) {
if(root == null){
return true;
}
if(maxDexth(root) == -1){
return false;
}
return true;
}
int maxDexth(TreeNode root){
if(root == null){
return 0;
}
int left = maxDexth(root.left);
if(left == -1){
return -1;
}
int right = maxDexth(root.right);
if(right == -1){
return -1;
}
if(Math.abs(left - right) > 1){
return -1;
}
return 1 + Math.max(left, right);
}
}
Python
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def isBalanced(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
if not root:
return True
if self.maxDepth(root) == -1:
return False
return True
def maxDepth(self, root):
if not root:
return 0
left = self.maxDepth(root.left)
if left == -1:
return -1
right = self.maxDepth(root.right)
if right == -1:
return -1
if abs(left - right) > 1:
return -1
return 1 + max(left, right)
C++
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isBalanced(TreeNode* root) {
if (!root) {
return true;
}
if (maxDepth(root) == -1) {
return false;
}
return true;
}
int maxDepth(TreeNode* root) {
if (!root) {
return 0;
}
int left = maxDepth(root->left);
if (left == -1) {
return -1;
}
int right = maxDepth(root->right);
if (right == -1) {
return -1;
}
if (abs(left - right) > 1) {
return -1;
}
return 1 + max(left, right);
}
};
